À propos des coniques
Re: À propos des coniques
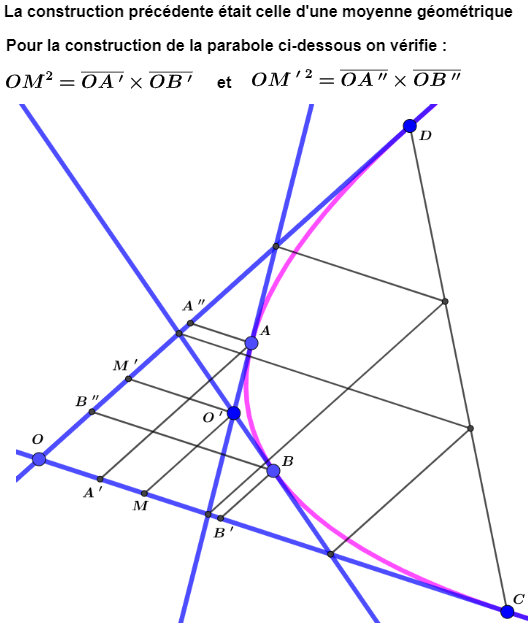
Ecrit le 20 mai23, 06:39Ici ci-dessous une construction d'une parabole à partir de trois points A,B,O
tels que les droites (OA) et (OB) sont deux de ses tangentes
A et B les points de contacts de ces deux tangentes avec la parabole
On utilisera la notion de sous-tangente en un point de la conique avec la définition donnée en dessous de la figure sachant que le sommet S (sur la figure) d'une parabole est le milieu de toute sous-tangente et pour le reste tout ce qui a été dit ici permet de retrouver cette construction
Voilà sur ce sujet tout ce qui peut être dit en introduction à propos des coniques
Définitions de sous-tangente et sous-normale :
La tangente en A d'une conique propre coupe l'axe focal en un point T et sa normale en un point N
A' la projection orthogonale de A sur l'axe focal
Le segment [TA'] se nomme la sous-tangente en A
Le segment [A'N] se nomme la sous-normale en A
tels que les droites (OA) et (OB) sont deux de ses tangentes
A et B les points de contacts de ces deux tangentes avec la parabole
On utilisera la notion de sous-tangente en un point de la conique avec la définition donnée en dessous de la figure sachant que le sommet S (sur la figure) d'une parabole est le milieu de toute sous-tangente et pour le reste tout ce qui a été dit ici permet de retrouver cette construction
Voilà sur ce sujet tout ce qui peut être dit en introduction à propos des coniques

Définitions de sous-tangente et sous-normale :
La tangente en A d'une conique propre coupe l'axe focal en un point T et sa normale en un point N
A' la projection orthogonale de A sur l'axe focal
Le segment [TA'] se nomme la sous-tangente en A
Le segment [A'N] se nomme la sous-normale en A
Re: À propos des coniques
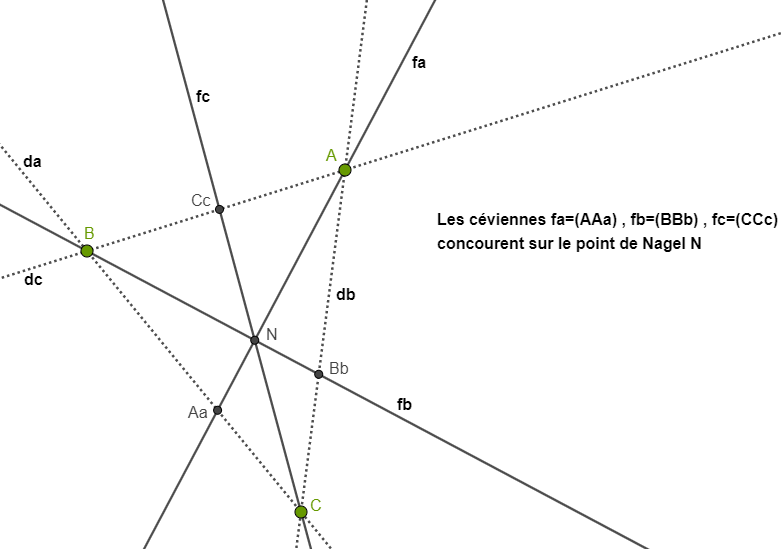
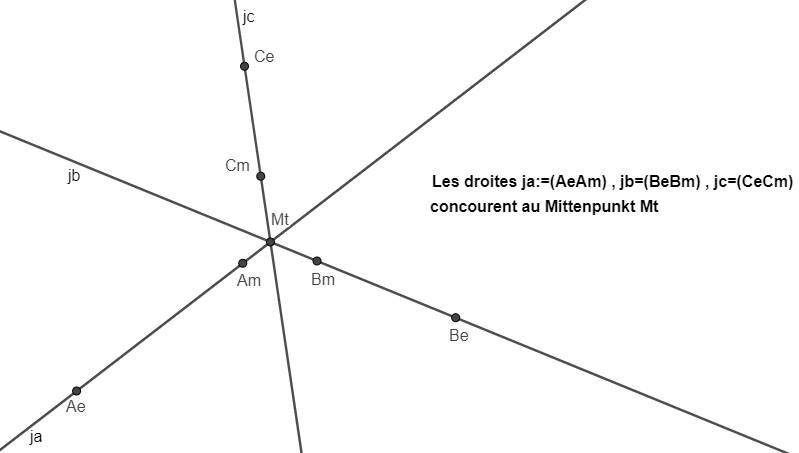
Ecrit le 29 juil.23, 08:52Les cercles sont aussi des coniques
Proposition de construction
Ajouté 3 heures 52 minutes 24 secondes après :
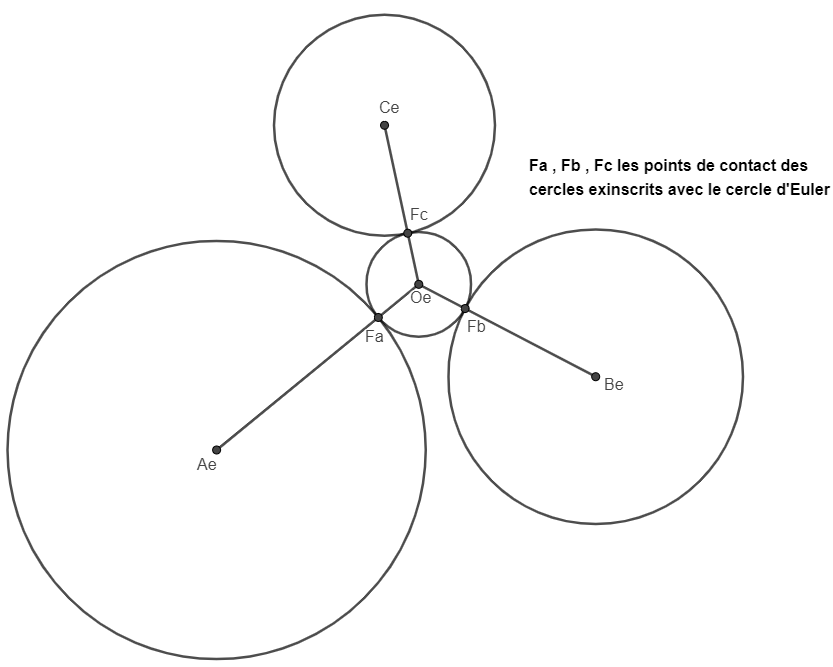
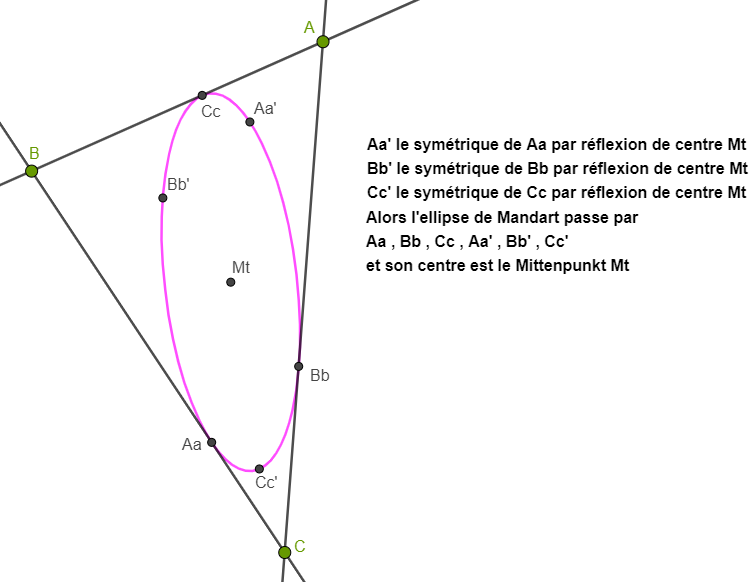
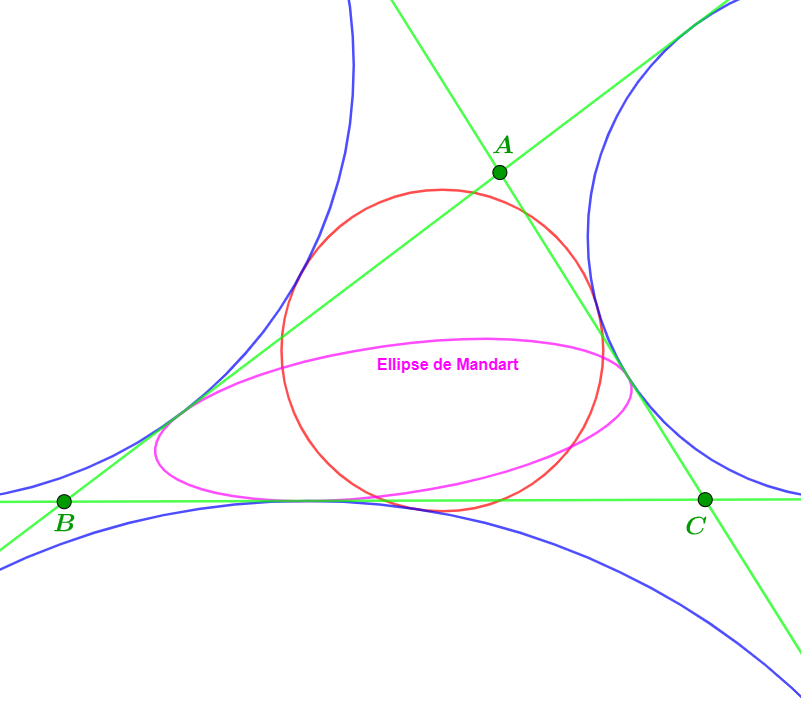
...et en agrandissant le centre de l'image précédente pour y faire apparaitre l'ellipse de Mandart
Ajouté 18 heures 30 minutes 58 secondes après :
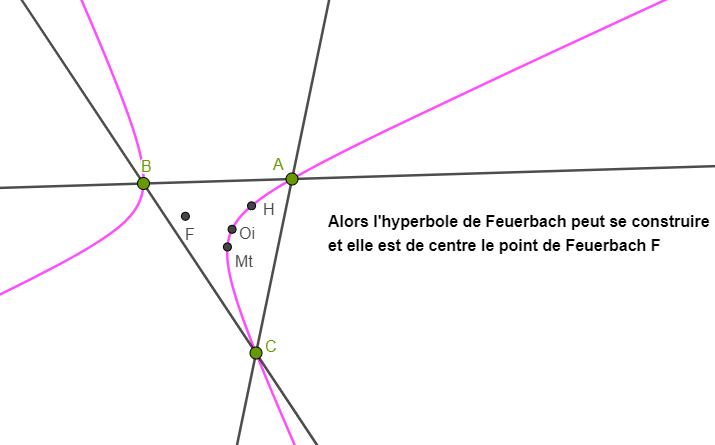
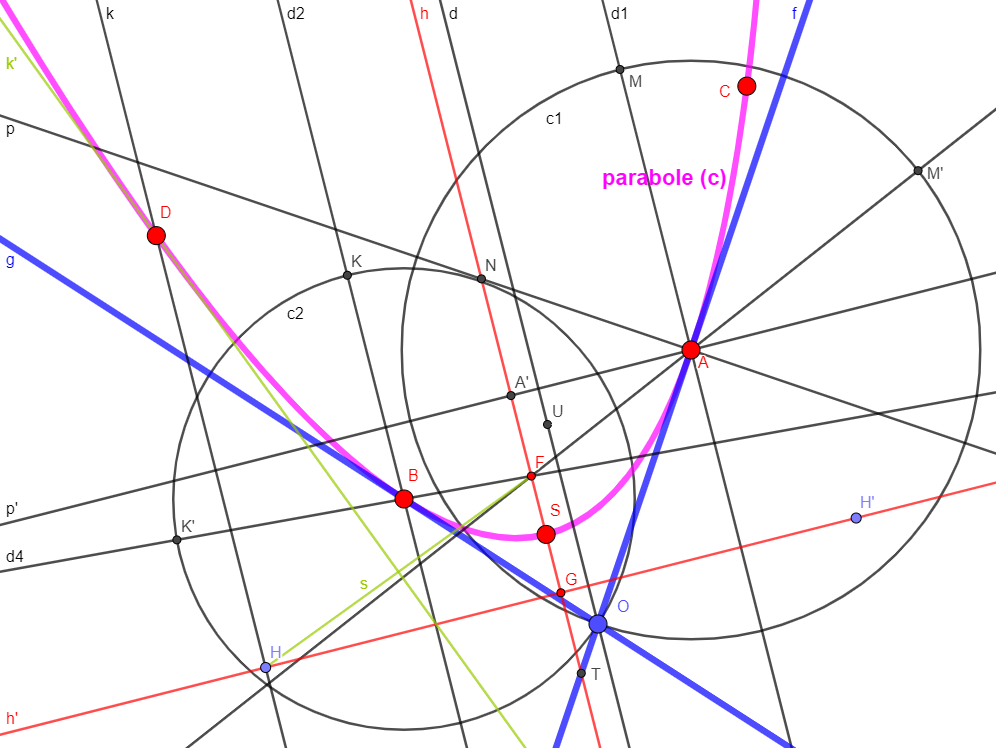
Une vue d'ensemble avec l'hyperbole de Feuerbach
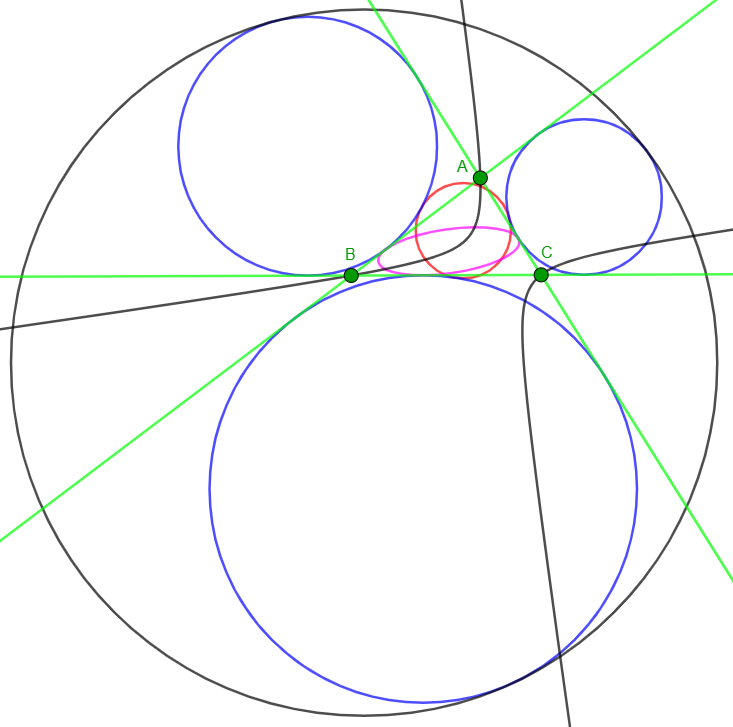
Proposition de construction

Ajouté 3 heures 52 minutes 24 secondes après :
...et en agrandissant le centre de l'image précédente pour y faire apparaitre l'ellipse de Mandart

Ajouté 18 heures 30 minutes 58 secondes après :
Une vue d'ensemble avec l'hyperbole de Feuerbach

Re: À propos des coniques
Ecrit le 03 août23, 09:03Bon alors il nous la fait JMI cette construction ?
(lui le scientifique qui dit que ceux qui croient en Dieu sont des cons )
Ajouté 15 heures 20 minutes 1 seconde après :
Bon alors en plusieurs jours
On va traiter le principe de la recherche des axes de symétrie des deux coniques
L'ellipse de Mandart et l'hyperbole de Feuerbach
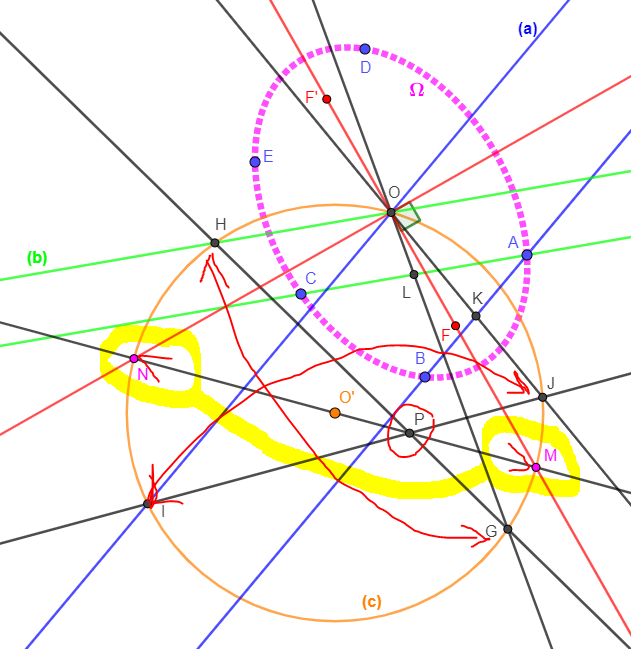
dans la figure ci-dessous les axes de symétrie de la conique à centre sont les droites (OM) et (ON)
on suppose qu'on a déjà construit le centre O (on verra plus tard )
On doit donc construire les deux points M et N
Pour ce faire on va se donner librement un point O' (un point déjà construit mais différent de O
et on trace le cercle de centre O' passant par O (le centre de notre conique)
eh bien ce cercle permet de définir une involution v de centre P c'est à dire que pour tout point X du cercle v(X) = X' et v(v(X))=X
où [XX'] est un diamètre du cercle et P est un point de ce segment [XX']
et ici v(M)=N et v(N)=M
et en consultant la première page de ce sujet dont je viens de copier cette image on construit facilement P donc la droite (O'P) qui coupe le cercle en M et N et cette construction s'effectue à l'aide de parallèles comme indiquées là-bas
Alors attention car il peut arriver que (et ça arrive ici quand on recherche les axes de symétrie de l'hyperbole de Feuerbach qu'en fait cette méthode ne fonctionne pas car P est dans le cas précédent l'intersection des deux droites (HG) et (IJ) mais ici malheureusement (HG) et (IJ) sont parallèles
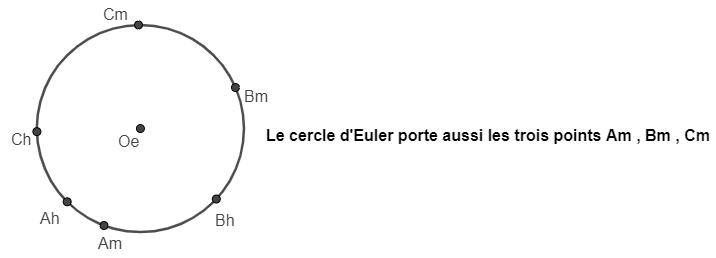
C'est normal car un théorème stipule que cette hyperbole est équilatère et cela à cause qu'elle porte l'orthocentre du triangle ABC et qu'elle porte aussi A,B,C
Alors ce n'est pas problématique car le fait que ces deux droites (HG) et (IJ) soient parallèles indique tout simplement que notre droite (O'P) est aussi parallèle à (HG) et (IJ)
(lui le scientifique qui dit que ceux qui croient en Dieu sont des cons )
Ajouté 15 heures 20 minutes 1 seconde après :
Bon alors en plusieurs jours
On va traiter le principe de la recherche des axes de symétrie des deux coniques
L'ellipse de Mandart et l'hyperbole de Feuerbach
dans la figure ci-dessous les axes de symétrie de la conique à centre sont les droites (OM) et (ON)
on suppose qu'on a déjà construit le centre O (on verra plus tard )
On doit donc construire les deux points M et N
Pour ce faire on va se donner librement un point O' (un point déjà construit mais différent de O
et on trace le cercle de centre O' passant par O (le centre de notre conique)
eh bien ce cercle permet de définir une involution v de centre P c'est à dire que pour tout point X du cercle v(X) = X' et v(v(X))=X
où [XX'] est un diamètre du cercle et P est un point de ce segment [XX']
et ici v(M)=N et v(N)=M
et en consultant la première page de ce sujet dont je viens de copier cette image on construit facilement P donc la droite (O'P) qui coupe le cercle en M et N et cette construction s'effectue à l'aide de parallèles comme indiquées là-bas
Alors attention car il peut arriver que (et ça arrive ici quand on recherche les axes de symétrie de l'hyperbole de Feuerbach qu'en fait cette méthode ne fonctionne pas car P est dans le cas précédent l'intersection des deux droites (HG) et (IJ) mais ici malheureusement (HG) et (IJ) sont parallèles
C'est normal car un théorème stipule que cette hyperbole est équilatère et cela à cause qu'elle porte l'orthocentre du triangle ABC et qu'elle porte aussi A,B,C
Alors ce n'est pas problématique car le fait que ces deux droites (HG) et (IJ) soient parallèles indique tout simplement que notre droite (O'P) est aussi parallèle à (HG) et (IJ)

Re: À propos des coniques
Ecrit le 29 août23, 20:32p-----n GROS MOT
J'ai un ultrafiltre
C'est ma faute à moi si les journées n'ont que 24h?
Oui! (j'ai l'habitude que ça sert à rien d'accuser les autres)

J'ai un ultrafiltre
C'est ma faute à moi si les journées n'ont que 24h?
Oui! (j'ai l'habitude que ça sert à rien d'accuser les autres)

Re: À propos des coniques
Ecrit le 08 sept.23, 13:06Notations toutes à refaire vu que >viewtopic.php?t=70521
- Saint Glinglin
- [ Aucun rang ]
- [ Aucun rang ]
- Messages : 25868
- Enregistré le : 11 févr.13, 22:07
-
Contact :
Re: À propos des coniques
Ecrit le 09 sept.23, 22:50Ah oui je m'en rappelle Saint GLINGLIN j'ai déjà entendu ce morceau mais bien bien avant internet (c'est bizarre je n'arrive pas à me rappeler où et quand)
Re: À propos des coniques
Ecrit le 29 oct.23, 05:46Je reviendrai plus tard sur ces constructions mais avant je propose ces objets :
Les octas (géométrie) du grec ancien oktô "huit" et τάσσω "arranger"
Un octas (s'écrit aussi avec un "s" au singulier) est une figure du plan affine composée de huit points A,B,C,A',B',C',D',E' tels que ABC est un triangle non plat et tels que :
A' appartient à la droite (BC), B' appartient à la droite (CA), C' appartient à la droite (AB), D' appartient à la droite (AB), E' appartient à la droite (AC)
C'est une figure de géométrie affine (du plan affine) qui possède une structure "conique" et donc très utile en géométrie projective
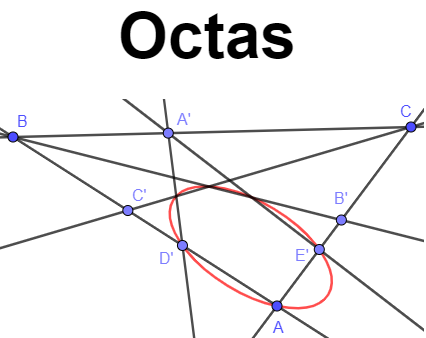
En rouge une ellipse à cause de la "structure conique des octas"
Observez les points d'intersection des droites et le passage de l'ellipse
Il faut comprendre que seuls cinq points définissent une conique et sur la figure la conique passe sur six points d'intersection
La "structure conique des octas" permet cela
Dans certaines configurations l'octas porte une hyperbole (c'est aussi une conique) ou bien porte une parabole (c'est aussi une conique) ou bien porte une conique dégénérée
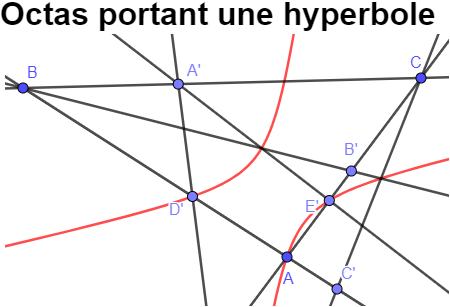
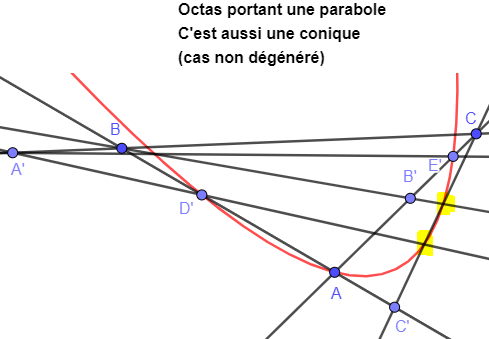
Les octas (géométrie) du grec ancien oktô "huit" et τάσσω "arranger"
Un octas (s'écrit aussi avec un "s" au singulier) est une figure du plan affine composée de huit points A,B,C,A',B',C',D',E' tels que ABC est un triangle non plat et tels que :
A' appartient à la droite (BC), B' appartient à la droite (CA), C' appartient à la droite (AB), D' appartient à la droite (AB), E' appartient à la droite (AC)
C'est une figure de géométrie affine (du plan affine) qui possède une structure "conique" et donc très utile en géométrie projective

En rouge une ellipse à cause de la "structure conique des octas"
Observez les points d'intersection des droites et le passage de l'ellipse
Il faut comprendre que seuls cinq points définissent une conique et sur la figure la conique passe sur six points d'intersection
La "structure conique des octas" permet cela
Dans certaines configurations l'octas porte une hyperbole (c'est aussi une conique) ou bien porte une parabole (c'est aussi une conique) ou bien porte une conique dégénérée


-
- Sujets similaires
- Réponses
- Vues
- Dernier message
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités