Religions du monde :: forum religion

Les perles : le Baccalauréat

« Le triangle est un rectangle avec un côté en moins. »

Les perles : le Baccalauréat

« Une ligne peut être perpendiculaire, droite, parallèle, courbe… Mais c’est pas elle qui décide. »

Les perles : à l’école

« L’ovale est un cercle presque rond, mais quand même pas. ».

_________________________________

Ne doute jamais de tes capacités en math, certains apparemment croient qu'un rond, est un truc ovale mais pas trop. Lol

Euclide s'en retournerait dans sa tombe si tu te dévalorisais aero.

Merci Uzzi et Indian



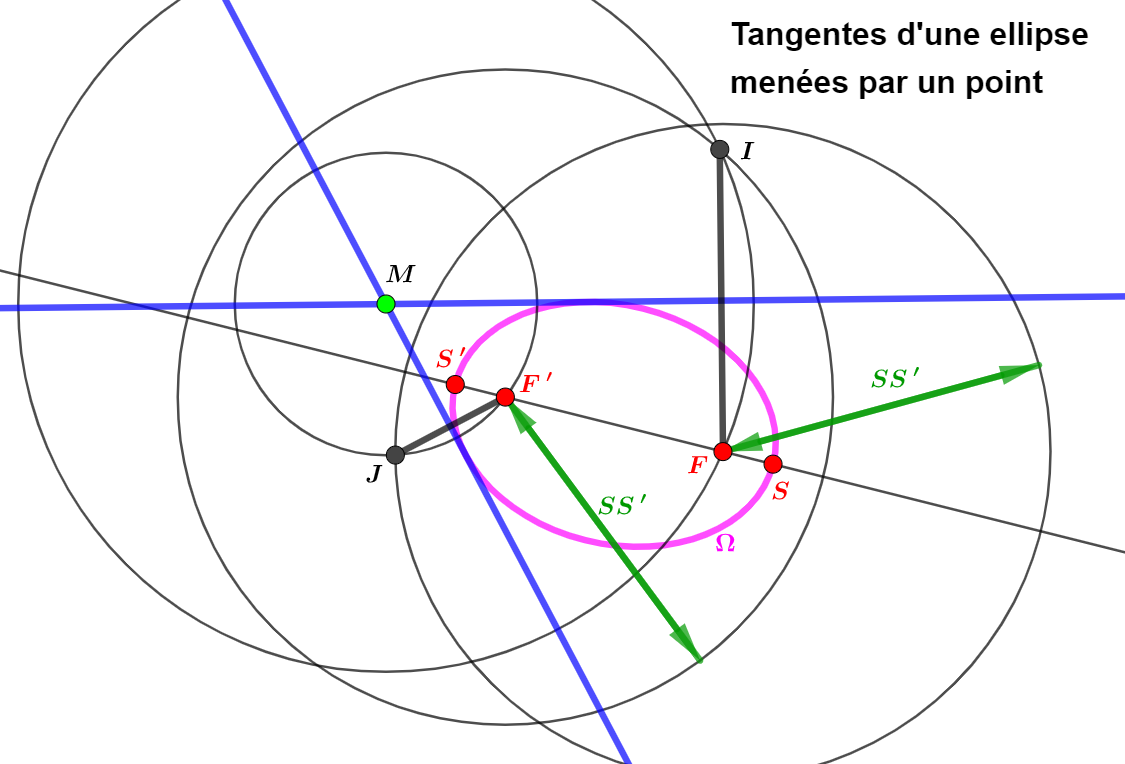Toutes ces constructions ainsi présentées ne nécessitent pas de connaissances particulières
Il suffit juste de les réaliser comme elles sont indiquées
Prendre un compas et une règle non graduée (aucune mesure n'est effectuée)
J'ai essayé ici de bien prendre soin à le faire sans l'utilisation d'un jargon abscons non accessible à tous

aerobase a écrit : ↑03 févr.23, 02:23 Merci Uzzi et Indian

Vraiment encore merci Indian
(merci car ça évite l'accumulation des réponses sur un même post)

Après la parabole et l'ellipse ici pour l'hyperbole



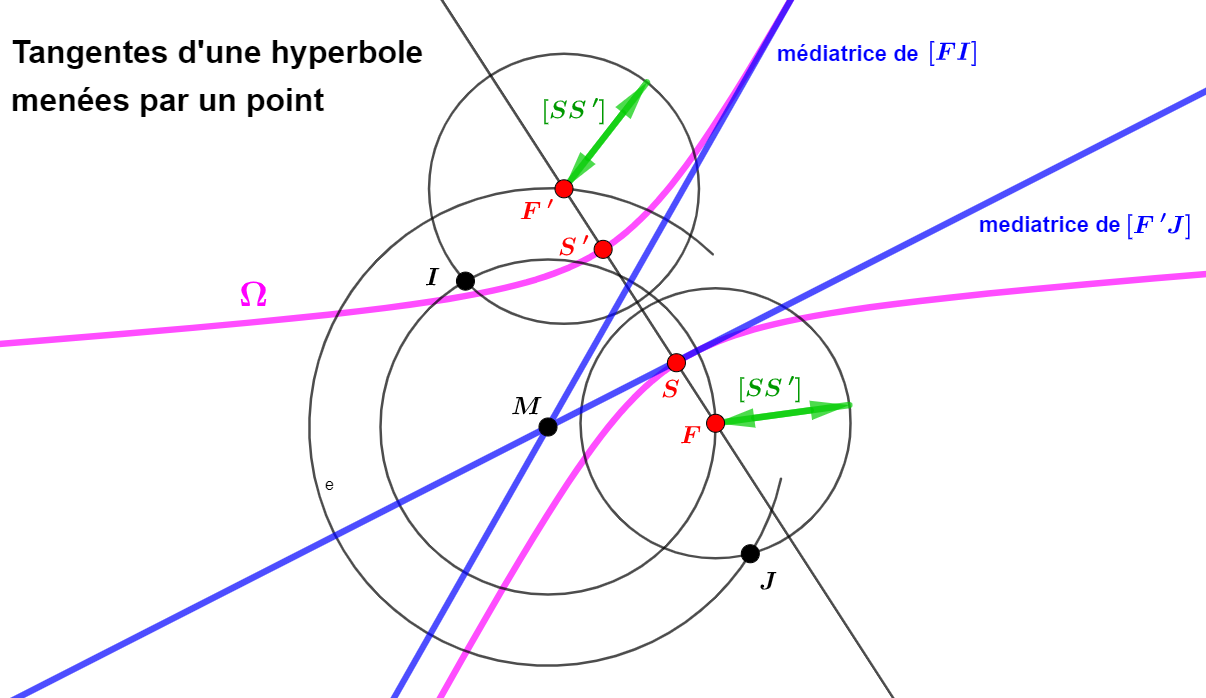Toutes ces constructions ainsi présentées ne nécessitent pas de connaissances particulières
Il suffit juste de les réaliser comme elles sont indiquées
Prendre un compas et une règle non graduée (aucune mesure n'est effectuée)
J'ai essayé ici de bien prendre soin à le faire sans l'utilisation d'un jargon abscons non accessible à tous

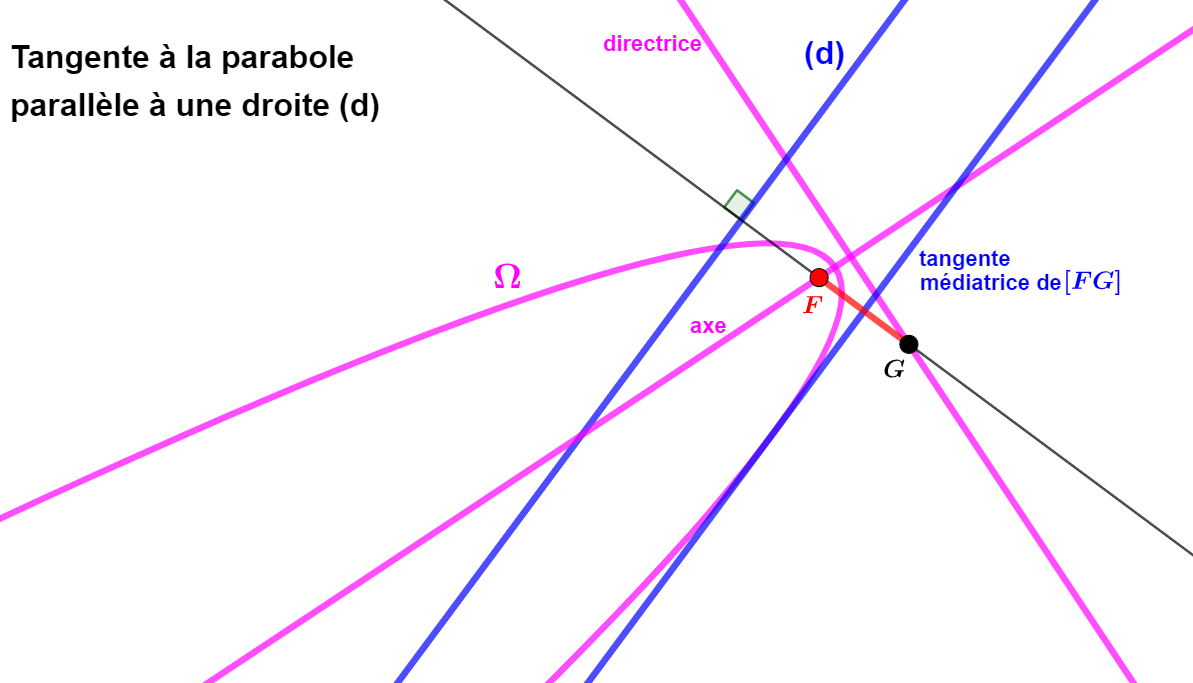
la parabole est fascinante aussi

peut être Indian ... peut être...
(merci pour le renouvellement des réponses)

wow j'adore ce fil

Merci Indian

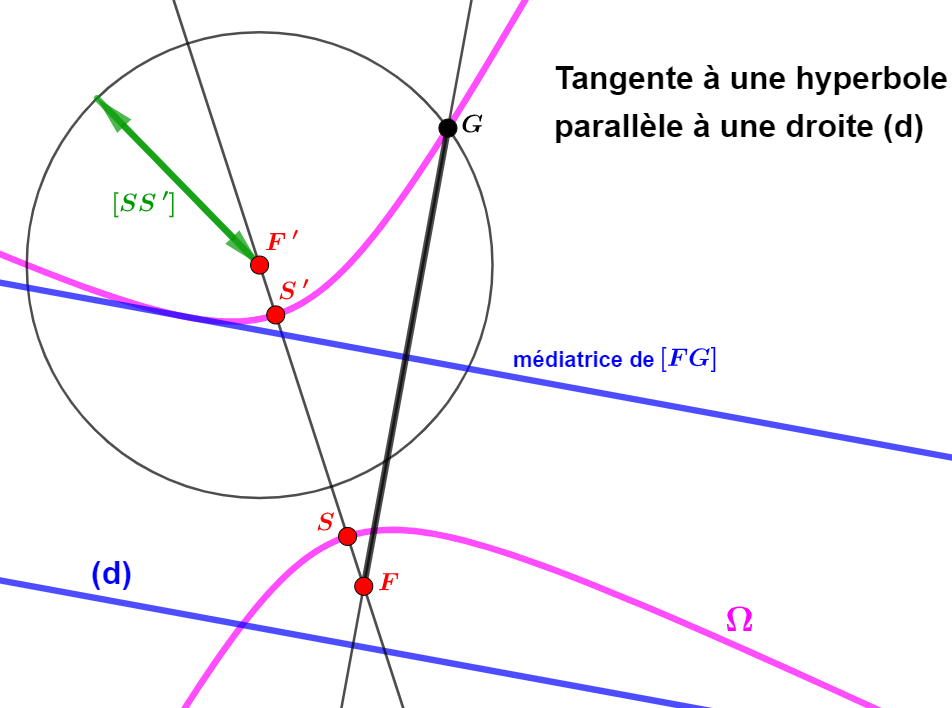
Ah je n'avais pas saisi cette subtilité !

Bien vu Aero.

Ajouté 26 minutes 26 secondes après :
mais évidemment là c'est un aparté

Ajouté 31 minutes 29 secondes après :
Bon le lecteur on a vu comment trouver le ou les foyers à partir de cinq points et on a vu les tangentes
et tout ça sans l'utilisation d'un jargon car ce sujet doit être accessible à tous
Il suffit d'avoir un compas et une règle non graduée (les graduations ne servent strictement à rien ici)
Maintenant et toujours dans cet esprit de partage sans avoir à chararabier
On va passer au brouillon projet de Desargues
Alors je fais grâce à l'éventuel lecteur de la "langue de bois" (au sens littéral et non péjoratif) de Désargues mais je place quand même un lien pour celui qui aime les jolies lettres
https://gallica.bnf.fr/ark:/12148/bpt6k105071b.image
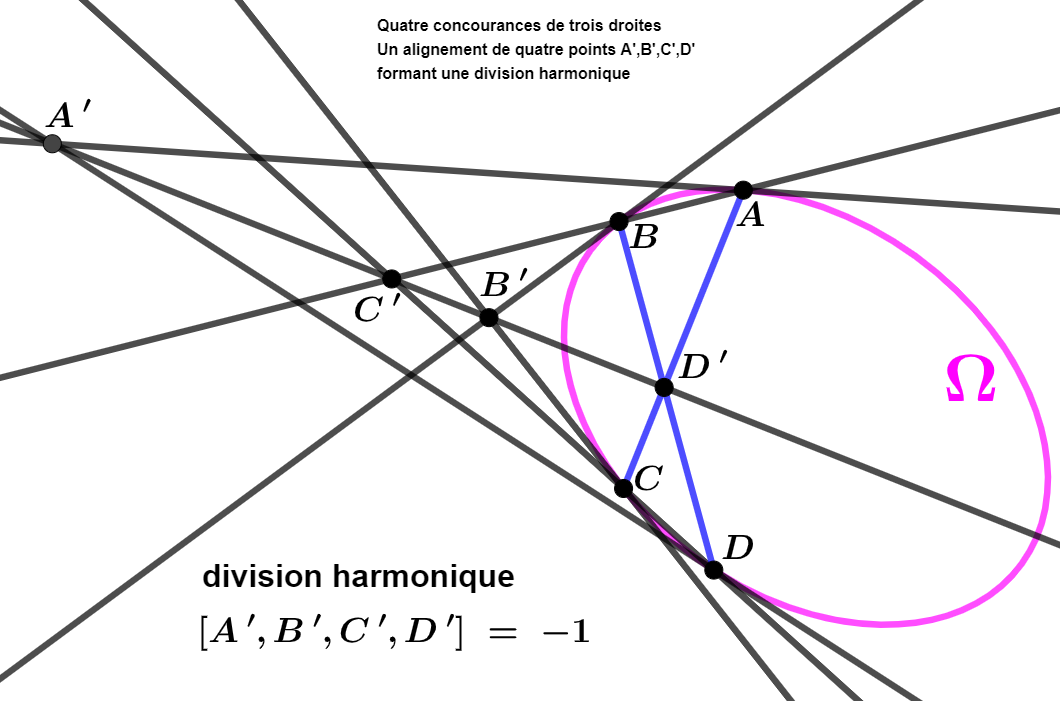
Dans la figue précédente on voit que j'ai écrit un petit jargon du genre [W,X,Y,Z]=-1 pour parler de division harmonique
mais bon à part ça on peut tracer ce qui est figuré (à part évidemment l'ellipse qui n'est là que pour visualiser la chose)
Je vais quand même détailler ce jargon mais là encore sans utiliser de charabia
Pas de charabia expliquant un charabia
En attendant je laisse le lien wiki de ce Girard Desargues
https://fr.wikipedia.org/wiki/Girard_Desargues

Ajouté 40 minutes 19 secondes après :
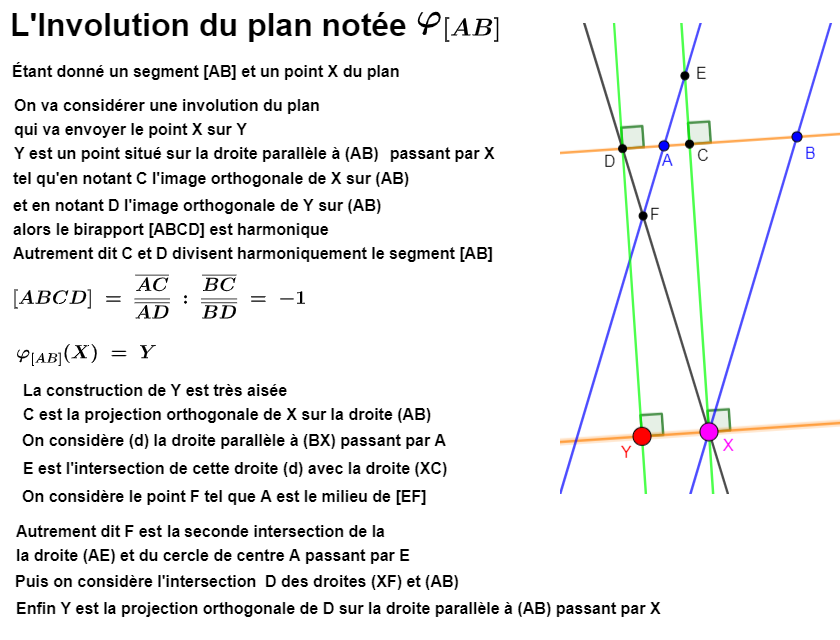
alors comme j'ai dit c'est uniquement visuel
pas de charabia et là on a une transformation appelée "involution" (j'y reviendrai)
en attendant toujours prendre une règle un compas et on a fabriqué une division harmonique (située sur la droite au dessus)
et ici en plus une involution du plan

Ceci n est pas un post.

Mic a écrit : ↑07 févr.23, 07:15 Ceci n est pas un post.

Pas mal.

J'm'interroge a écrit : ↑07 févr.23, 07:25 Pas mal.

Mais si tu te rappelles bien sur le tchat tu m'avais demandé de t'expliquer à propos du rapport harmonique et là entre autre j'ai préféré faire ça sans aucun jargon

Je ne sais toujours pas si ça te suffit comme explication car là tu réponds à Mic

(le seul jargon employé jusqu'à ici c'est uniquement celui-là [WXYZ]=-1)

PS : Étant entendu que tu ne voulais pas qu'on te parle de mesure algébrique ni de produit scalaire