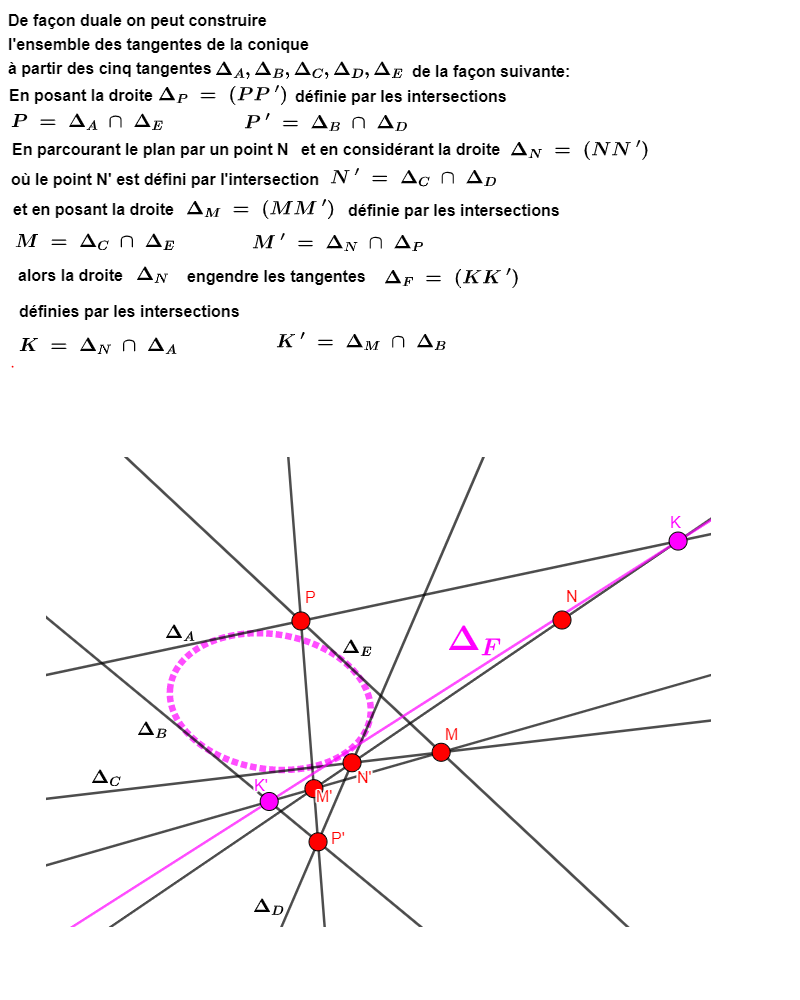
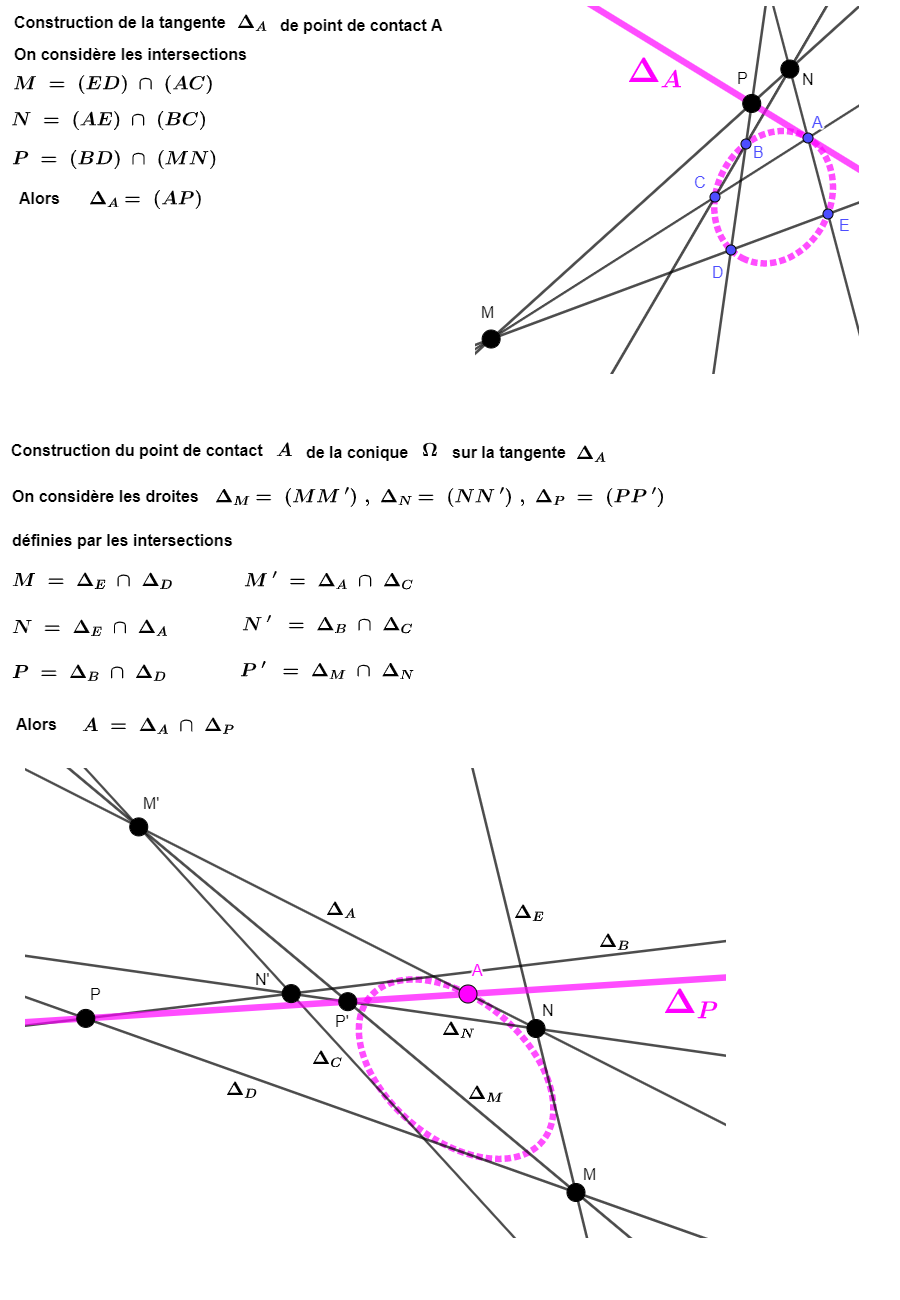
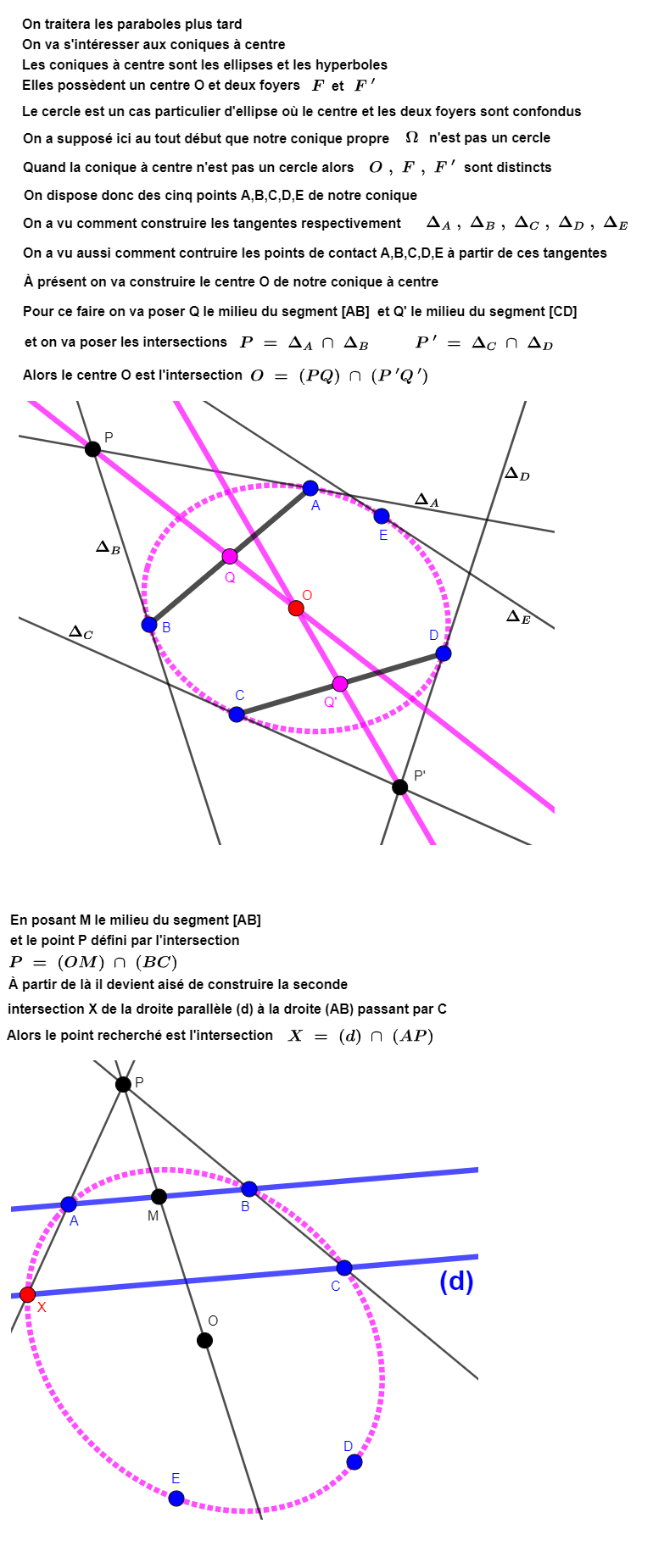
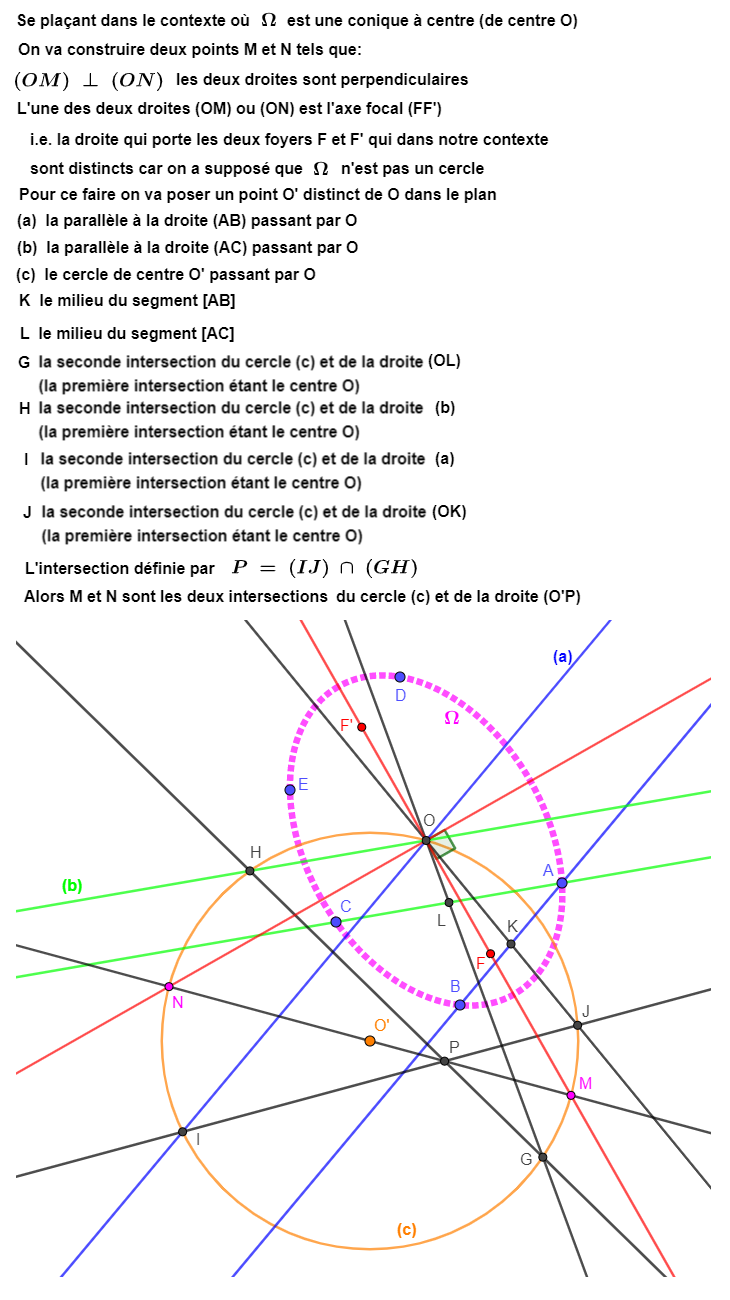
keinlezard a écrit : ↑31 janv.23, 23:53
Hello,
Renouvellement

Cordialement
Merci Keinlezard
Bon juste avant de parler d'un des théorèmes d'Apollonius de Perga
Un petit aparté:
Pour moi tous ceux qui sont venus après lui n'ont fait que redécouvrir ce qu'il avait trouvé
Voyons voir un peu ce qu'il nous dit dans son traité sur les coniques
Là dans ce lien
https://gallica.bnf.fr/ark:/12148/btv1b9001431j.image à la page 153

Si ça ce n'est pas une sphère de Dandelin bah je veux bien aller en Enfer
Comparons avec ce que nous dit la version officielle sur la découverte des sphères de Dandelin (XIX ième siècle)
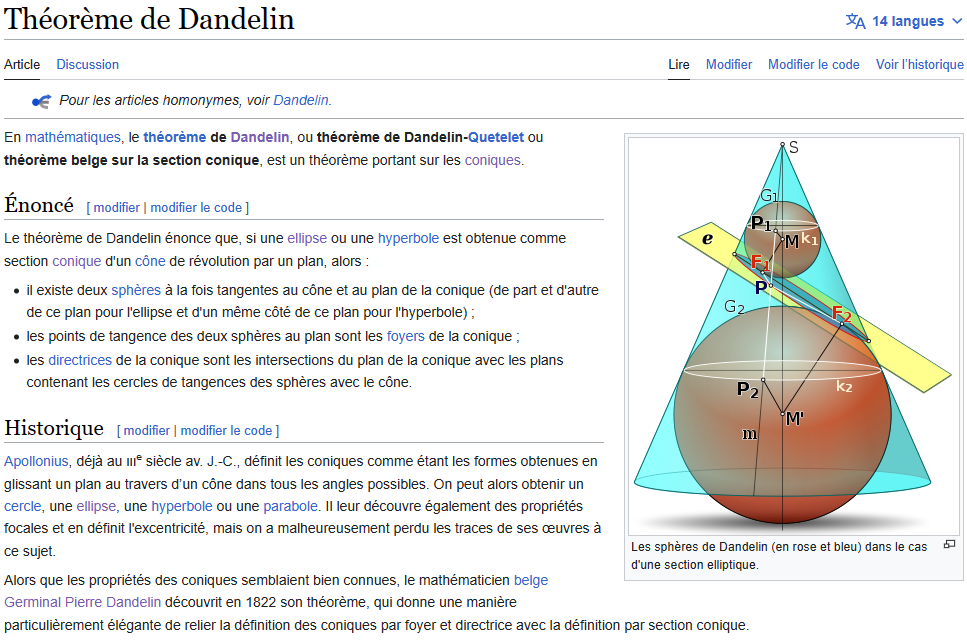
Juste mon avis mais qui n'engage que moi :
Dandelin n'a fait que découvrir ce que les anciens connaissaient mais que l'histoire oublia pendant plusieurs siècles
Mais bon on s'en fout on verra ça plus tard ....
Alors de quoi s'agit-il ici?
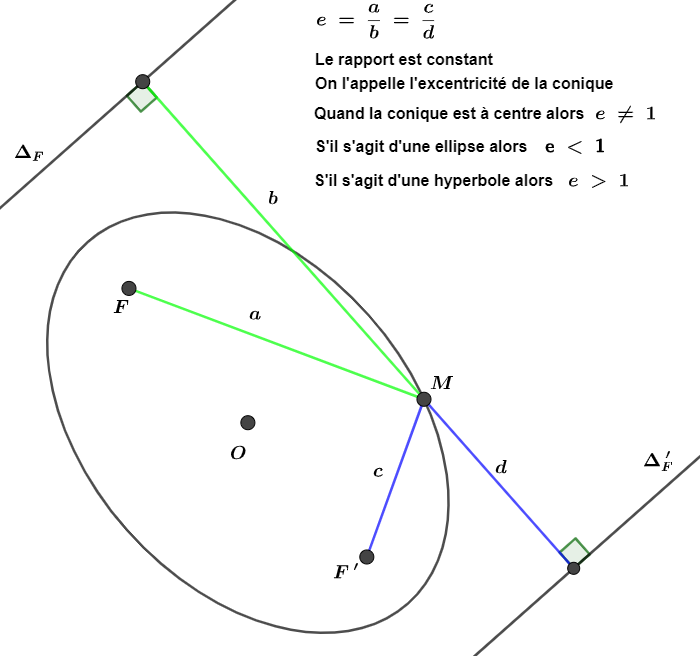
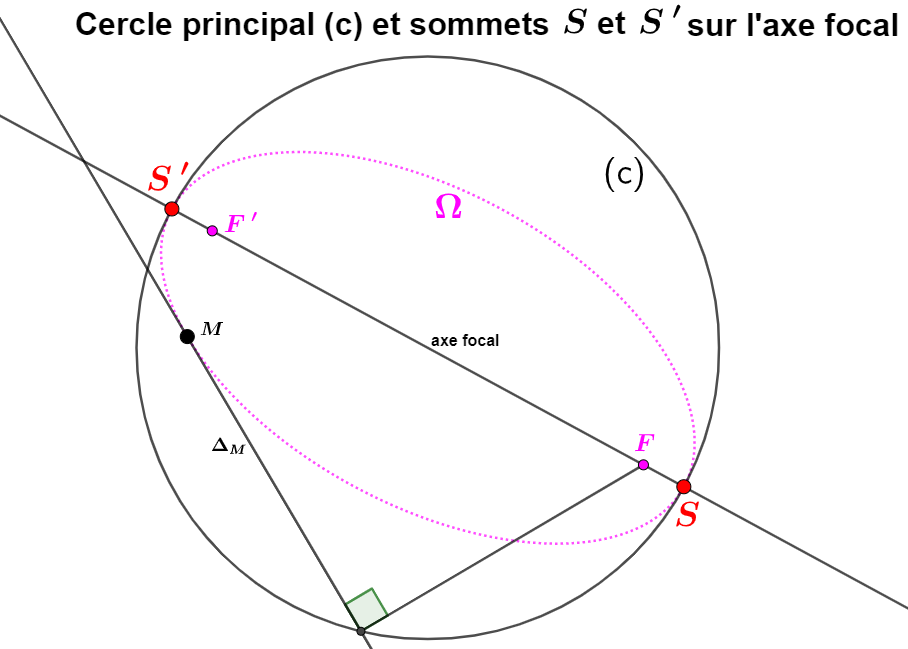
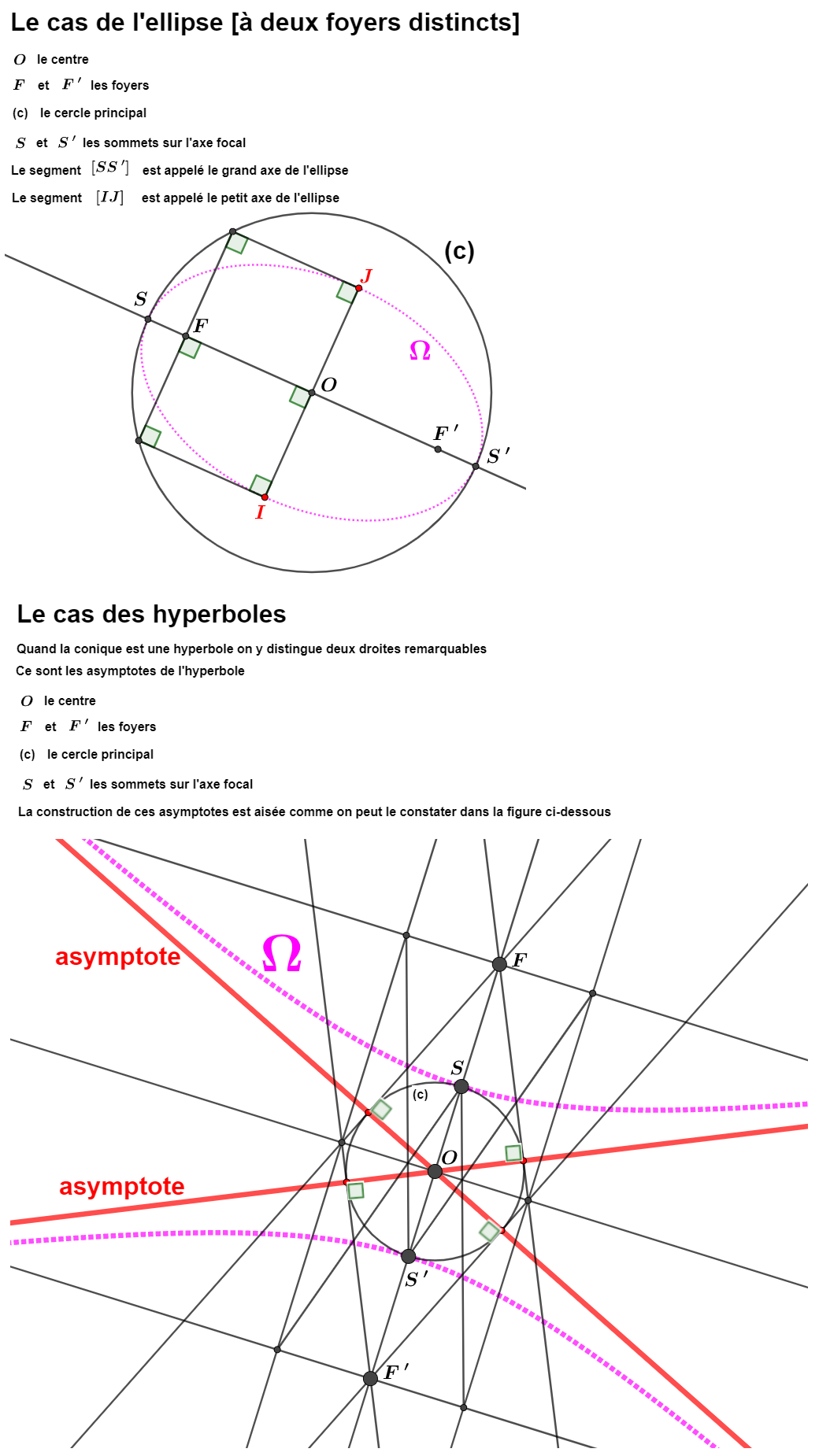
Apollonius (donc au IIIième siècle avant Jésus Christ) avait remarqué que pour toute conique à centre à deux foyers
distincts il existe deux droites remarquables appelées directrices
Chacune de ces directrices est associée à un foyer
Une directrice associée au foyer F et une autre associée au foyer F'
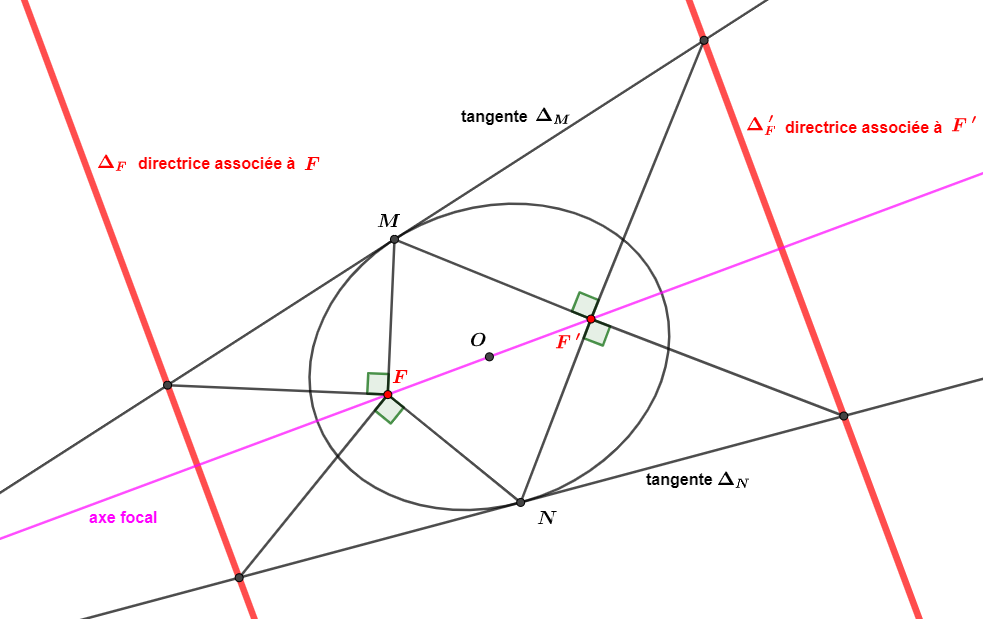
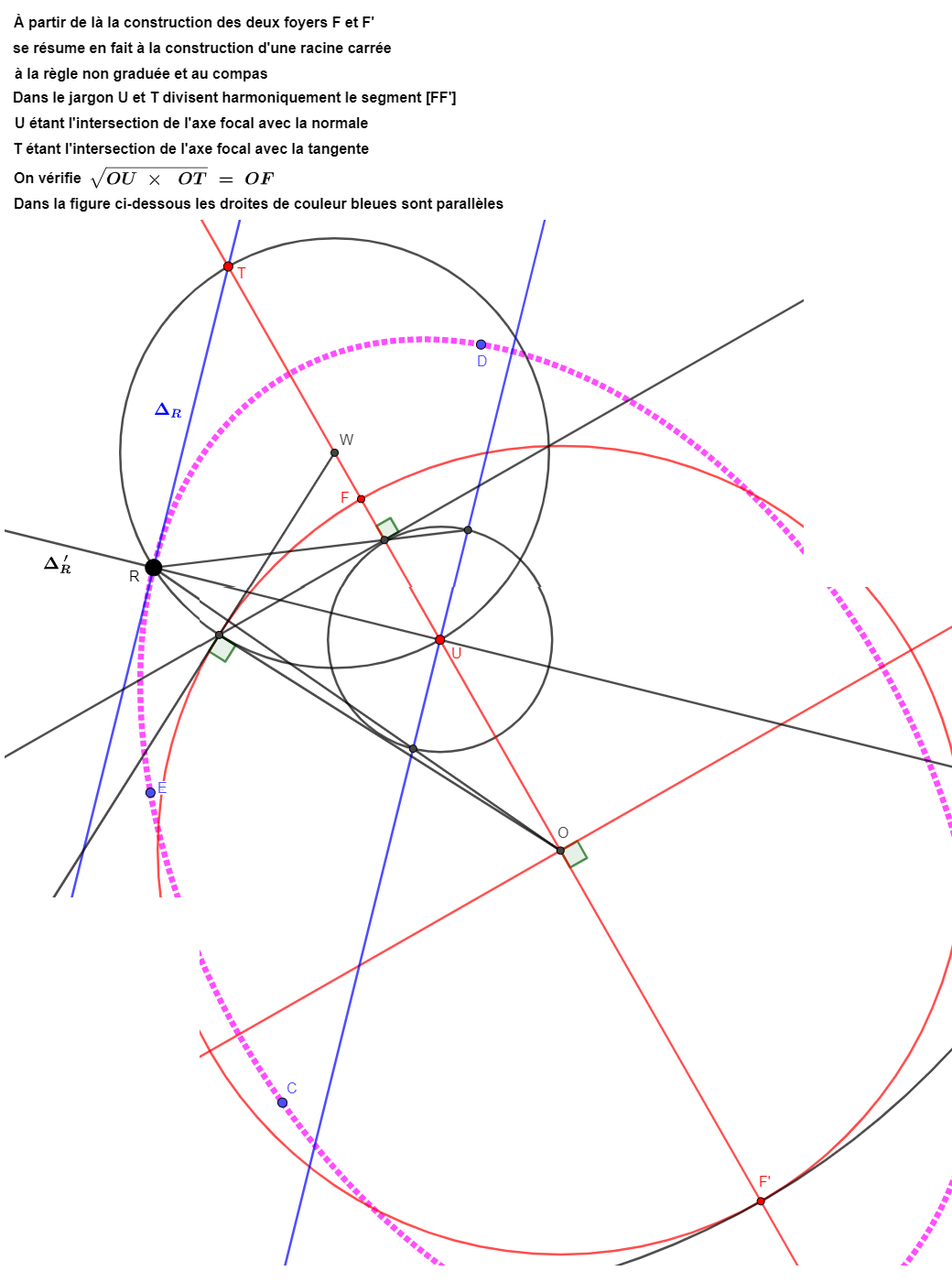
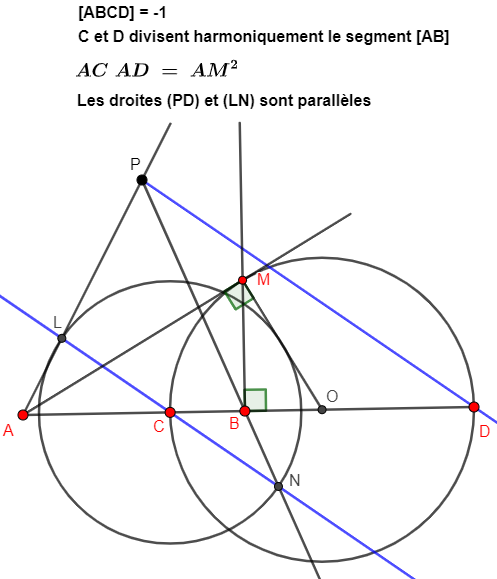
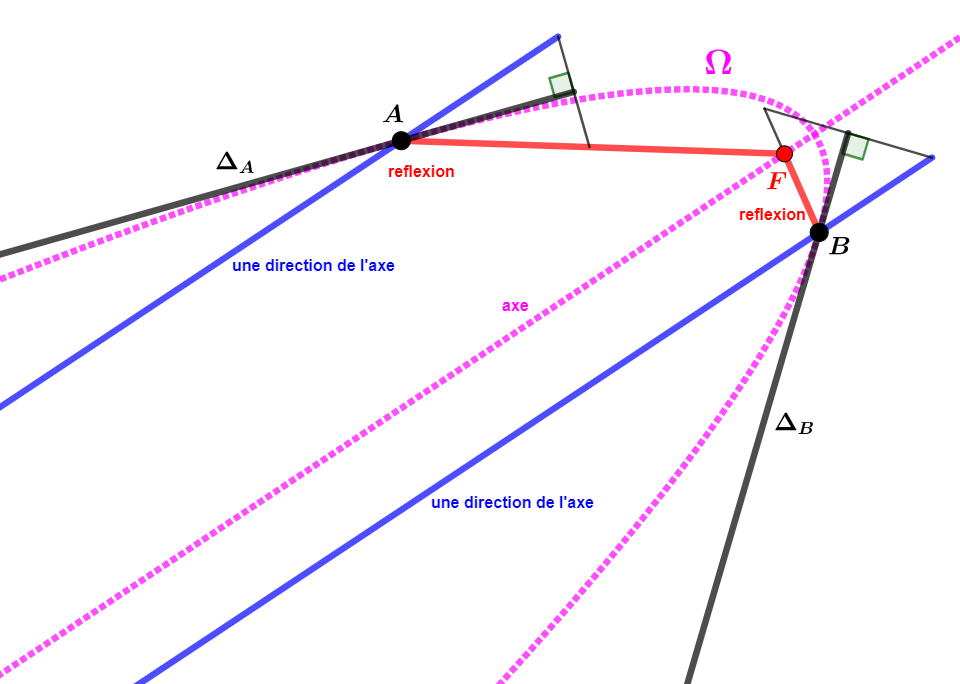
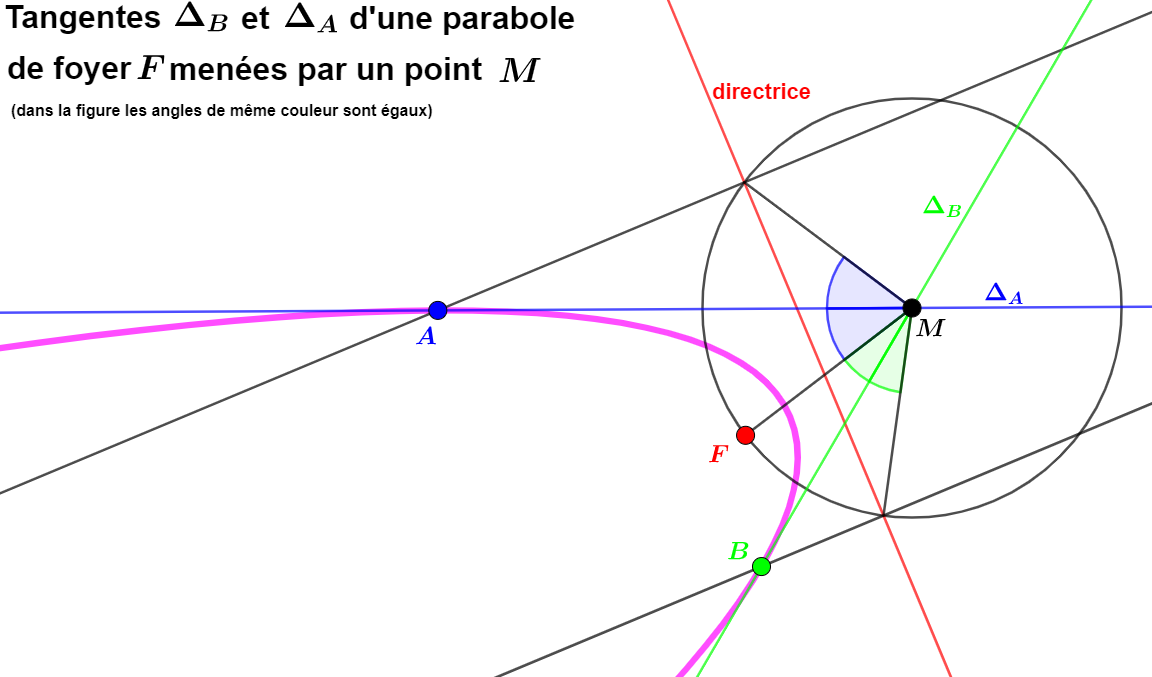
Le théorème d'Apollonius stipule que la droite perpendiculaire sur un foyer au segment [MF] est sécante à la tangente en un point de cette droite
Il avait remarqué que le lieu de rencontre de ces deux droites est une droite (la directrice associée à F)
idem pour [MF'] pour la directrice associée à F'
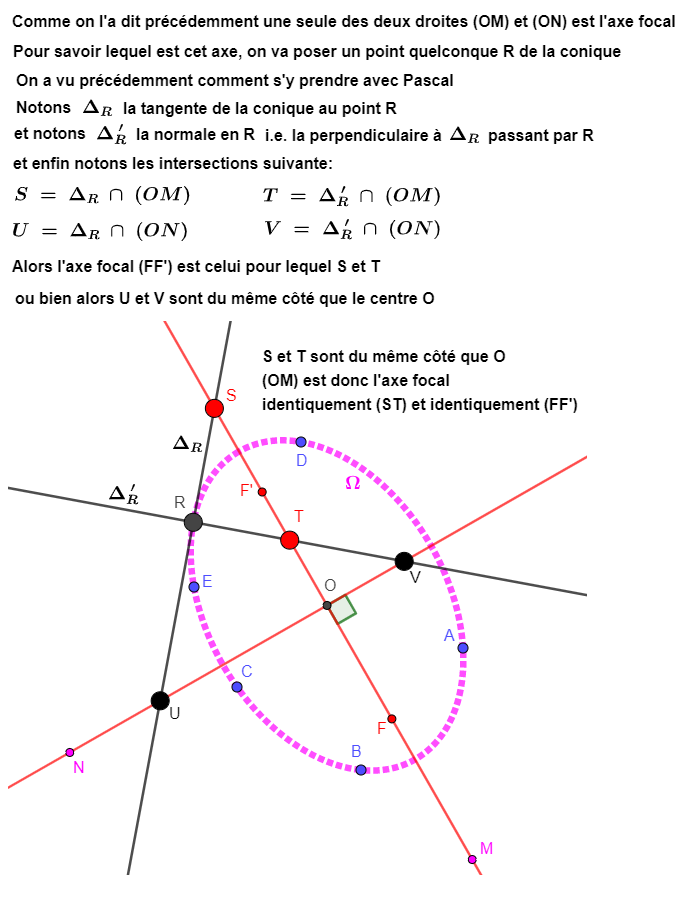
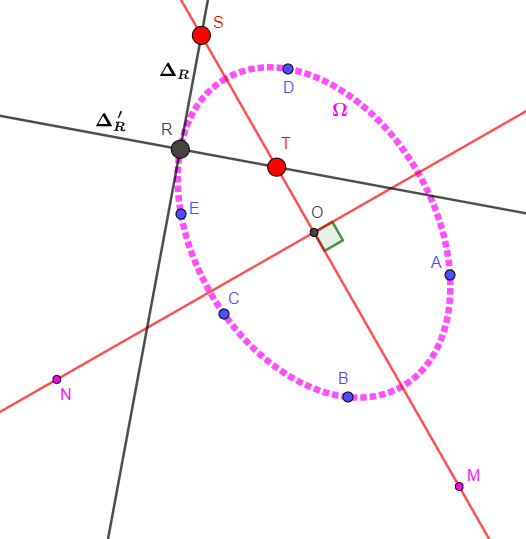
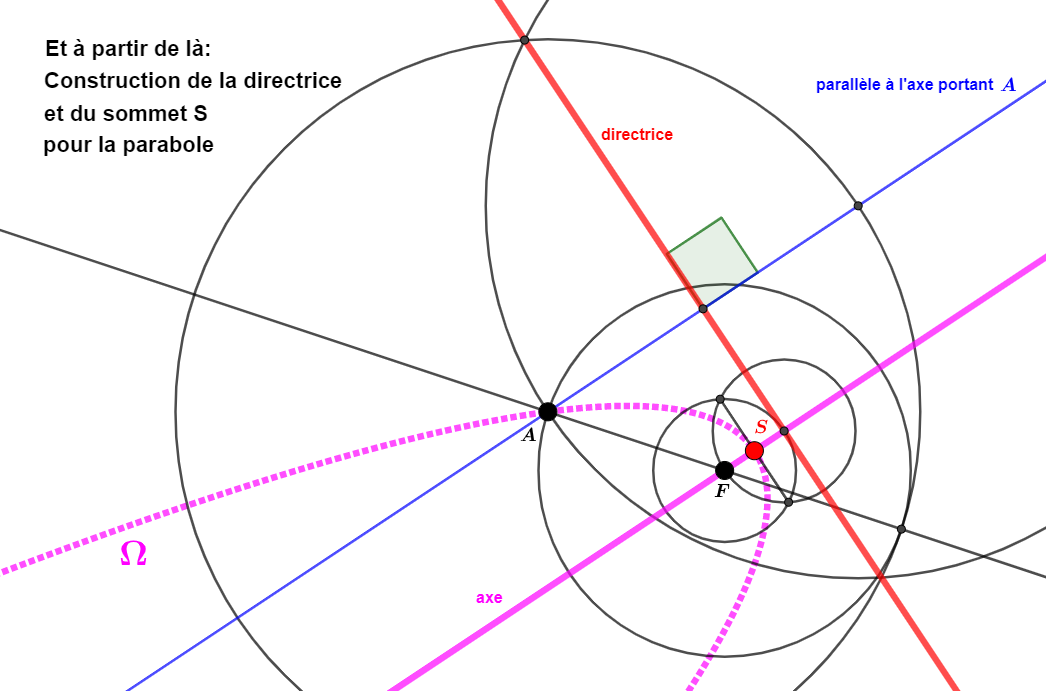
Voyons ci-dessous comment construire ces deux directrices
Ci-dessous par Pascal on se donne deux points M et N sur la conique (on n'est donc pas obligé de prendre les cinq points A,B,C,D,E initialement donnés) et la tangente pour chacun de ces deux points lesquels sont les points de contact avec la conique
La figure de construction est simple et se passe de commentaires