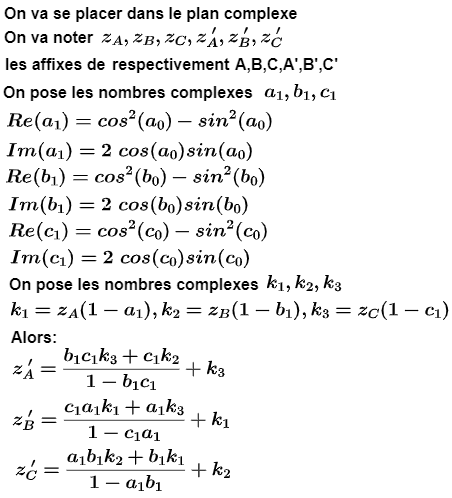Page 1 sur 2
Nombre d'or (proposé par Michel Bataille)
Posté : 20 oct.23, 04:25
par aerobase
Re: Nombre d'or (proposé par Michel Bataille)
Posté : 20 oct.23, 04:28
par J'm'interroge
Pas mal !
Je ne connaissais pas cette construction.
.
Re: Nombre d'or (proposé par Michel Bataille)
Posté : 20 oct.23, 04:43
par aerobase
J'm'interroge a écrit : ↑20 oct.23, 04:28
Pas mal !
Je ne connaissais pas cette construction.
.
Moi non plus
C'est de quelqu'un qui vivait à Rouen en 2011
ça date de 2011 sur un site de l'université Florida Atlantic University
https://www.fau.edu/
Re: Nombre d'or (proposé par Michel Bataille)
Posté : 20 oct.23, 04:56
par indian
peut on y ajouter un pentagone?
Re: Nombre d'or (proposé par Michel Bataille)
Posté : 20 oct.23, 05:03
par aerobase
Pourquoi pas Indian (il est chez lui)
Re: Nombre d'or (proposé par Michel Bataille)
Posté : 20 oct.23, 23:17
par J'm'interroge
Re: Nombre d'or (proposé par Michel Bataille)
Posté : 21 oct.23, 02:56
par prisca
Re: Nombre d'or (proposé par Michel Bataille)
Posté : 21 oct.23, 07:11
par aerobase
Ah faut croire Prisca
Re: Nombre d'or (proposé par Michel Bataille)
Posté : 21 oct.23, 13:12
par J'm'interroge
Ça n'a rien à voir mais je trouve que le 5ième terme de la fraction continue de Pi est étonnamment grand :
Pi = [3,7,15,1,292,1,1,1,2,1,3,1,…]
Re: Nombre d'or (proposé par Michel Bataille)
Posté : 24 oct.23, 03:15
par aerobase
sinon à part ça

Re: Nombre d'or (proposé par Michel Bataille)
Posté : 24 oct.23, 03:21
par J'm'interroge
.
Merci,
Je ne connaissais pas les cercles d'Apollonius ni les divisions harmoniques de segments.
Propriété intéressante de ce cercle.
.
Re: Nombre d'or (proposé par Michel Bataille)
Posté : 24 oct.23, 03:31
par aerobase
on prend un segment [AB] et on se donne un scalaire "s" ici dans cet exemple on a pris s le nombre d'or
Alors il existe un cercle appelé cercle d'Apollonius du triplet (A,B,s) tel que pour tout point M de ce cercle alors
MA/MB=s
Le calcul (géométrie analytique) de ce cercle se simplifie quand le scalaire "s" est le nombre d'or
Re: Nombre d'or (proposé par Michel Bataille)
Posté : 25 oct.23, 11:40
par aerobase
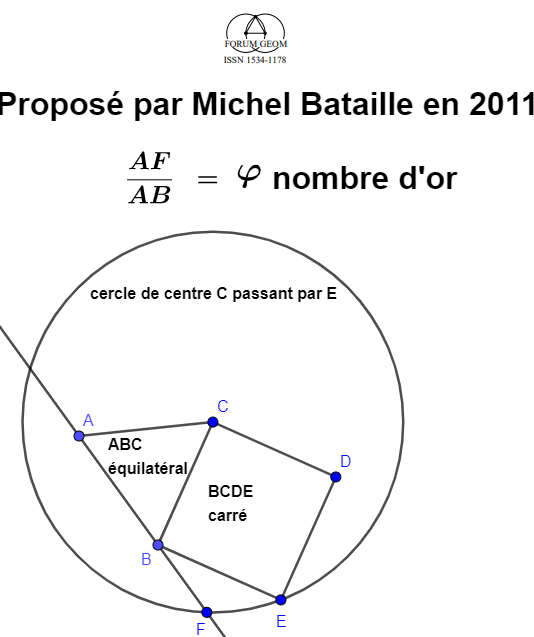
Dans ce sujet, Michel Bataille nous propose de construire le nombre d'or
à partir d'un triangle équilatéral
Par Frank Morley
https://fr.wikipedia.org/wiki/Frank_Morley
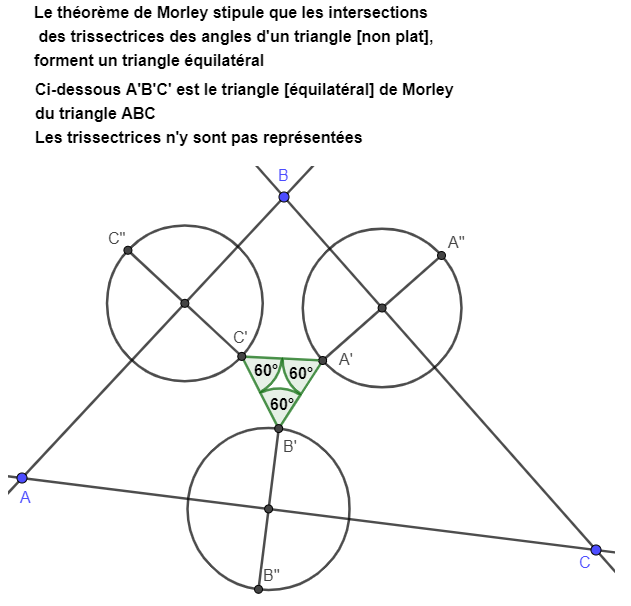
On se propose de faire correspondre un triangle équilatéral
à un triangle non plat quelconque en utilisant le théorème de Morley
On va utiliser la démonstration du théorème de Morley
donnée dans ce lien
http://www.numdam.org/item/PMIHES_1998__S88__43_0.pdf
par Alain Connes en 1998 pour déterminer les affixes respectivement za',zb',zc'
des sommets respectivement A',B',C' du triangle de Morley A'B'C' du triangle ABC

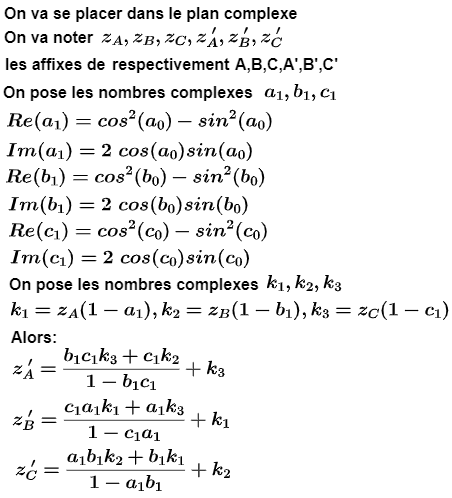
Re: Nombre d'or (proposé par Michel Bataille)
Posté : 26 oct.23, 09:53
par J'm'interroge
Up !
Re: Nombre d'or (proposé par Michel Bataille)
Posté : 26 oct.23, 09:57
par aerobase
Merci JMI
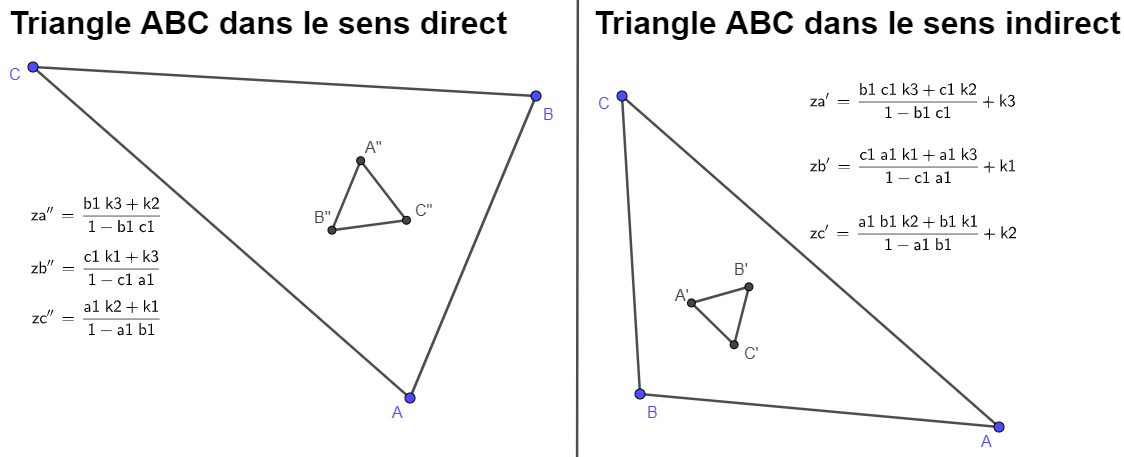
Les formules des affixes des sommets du triangle de Morley
dépendent du sens (direct ou indirect) du triangle ABC